2018年云南省事业单位考试—教案数学高中《指数函数的图像和性质》
云南华图教育 | 2018-07-04
分享
指数函数的图像及性质
张三莉
课型:新授课
课时:1课时
教学目标:
1、知识与技能目标
让学生会画指数函数的图像,能够根据图像归纳总结出指数函数的定义域、值域以及单调性等,并能够解决相应的实际问题。
2、过程与方法目标
通过自主画图、观察与总结,让同学经历由“特殊-一般-特殊”的认知过程,完善认知结构,掌握数形结合、分类讨论、归纳推理等数学思想方法。
3、情感、态度与价值观目标
让同学感受数学问题探索的乐趣和成功的喜悦,体会数学的严谨、理性之美,激发学生学习数学知识的兴趣。
教学重点:
归纳、总结指数函数的性质。
教学难点:
会应用指数函数的性质进行指数大小的比较。
教学工具(或教学准备):白纸、多媒体
教学过程:
一、创设情境,引入新课
1、复习旧知,引入新知
指数函数的定义是什么?定义中需要注意的问题是什么?在研究一个函数时,需要掌握函数的哪些要素?(寒素三要素为定义域、值域和对应法则;单调性反映了函数的值随自变量变化而产生变化的一种趋势。)
2、提出问题,探索新知
上节课让同学们画了y=2x、y=(1/2)x的图像,大家都画好了吗?仔细观察图像,你能总结出这两个图像的性质吗?
二、探索比较,掌握特征
(一)观察函数特点。
1、观察函数的定义域、值域和单调性;
2、观察函数其他特性。
(二)归纳特征,构建新知
1、通过观察图像可总结得出如下表格所示的指数函数的性质:
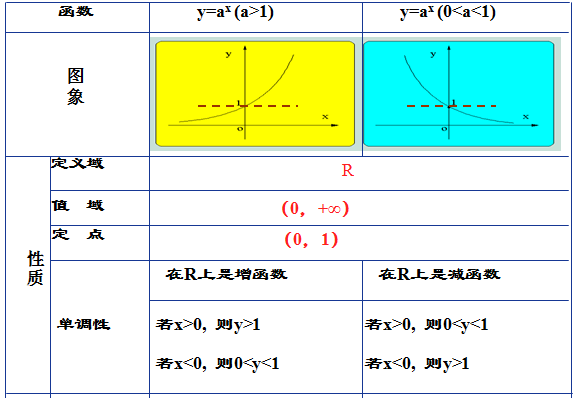
2、请同学们画出图像y=3x、y=(1/3)x的图像,和y=2x、y=(1/2)x的图像对比发现新的规律。
a. 底数互为相反数的两个对数函数关于y轴对称;
b. 当a大于1时,图像表现为底大图高;
当a大于0小于1时,图像表现为底大图低。
三、巩固与练习
(一)巩固
画出指数函数的图像性质表。
(二)练习
请同学们比较以下数的大小并说明原因:
y=1.55和y=1.52
y=0.85和y=0.82
y=0.8-5和y=0.8-2
四、小结体会
同学们,你觉得这节课里你表现怎样?你有什么收获和体会?
五、课后作业
比较a-3,a-2的大小。
分组讨论:是否能够用上述简单的方法进行比较。
板书设计:
指数函数的图像及性质
一般地,形如y=ax(a>1,a≠0)叫做指数函数,其中x是自变量,函数定义域为R。
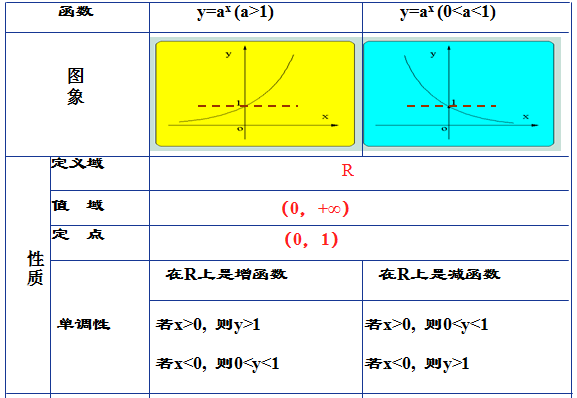

延伸阅读
